11357. Комната
Имеется комната размером n
* m. Найдите максимальное количество целых плиток размером k * k,
которые можно поместить в комнате.
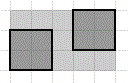
На рисунке изображен один из
возможных максимальных ответов для n = 5, m = 3, k = 2.
Вход. Первая строка содержит целое
число n (1 ≤ n ≤ 1000). Вторая строка содержит целое
число m (1 ≤ m ≤ 1000). Третья строка содержит целое
число k (1 ≤ k ≤ 1000).
Выход. Выведите максимальное количество
целых плиток размером k * k, которое можно поместить в комнату.
|
Пример
входа |
Пример
выхода |
|
5 3 2 |
2 |
РЕШЕНИЕ
математика
Анализ алгоритма
В комнату можно поместить (n / k) * (m / k)
целых плиток.
Пример
Рассмотрим
пример, в котором n = 7, m = 5, k = 2.
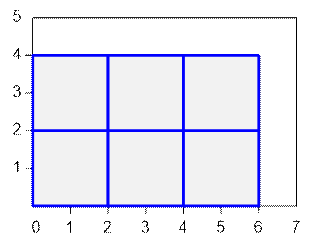
По горизонтали
имеется место для n / k = 7 / 2 = 3 квадратов, по вертикали – место для m / k = 5 / 2 = 2 квадратов. Всего число квадратов, которое
поместится в комнату, равно (n / k) * (m / k) = 3 * 2 = 6.
Реализация алгоритма
Читаем входные данные.
scanf("%d %d %d", &n, &m, &k);
Вычисляем и выводим ответ.
res = (n / k) * (m /
k);
printf("%d\n", res);
Java реализация
import java.util.*;
class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
int k = con.nextInt();
int res = (n / k) * (m / k);
System.out.println(res);
con.close();
}
}
Python реализация
Читаем входные данные.
n = int(input())
m = int(input())
k = int(input())
Вычисляем и выводим ответ.
res = (n // k) * (m
// k)
print(res)